You started taking vitamin-D a couple of weeks ago and you notice it takes you less time to fall asleep at night, is it a result of the vitamin D or is it something else, is there maybe something else that causes you to fall asleep more easily?
So you decide to do an experiment.
You take 50 coworker volunteers, and you split them to two groups, one 125coworker group will get vitamin D the same one you took, while the other group will take a placebo.
You notice that the guys who took the real vitamin did get shorter amount of time to fall asleep. Was it the vitamin D as the cause?
It could be, and it could also be the case that not, maybe they share a project they work on and it's going well, so they fall asleep better while the other ones are having hard time and it's not related therefore to any vitamin D they take or not.
This is where hypothesis testing and significance come into play.
Hypothesis testing is almost what we did here with the experiment, but we want to also know was the vitamin D correlated to the change in sleep behavior or not?
Basically we want to answer this question:
We calculate how unlikely was it for the sleep pattern to change, or was it likely and sleep patterns do change for these coworkers, so we cannot explain it with the vitamin D.
Because if sleep patterns change from time to time for our workers then it's not that of strange thing that it changed while taking the vitamin D in other words it's just a thing that happens.
We have two ways to estimate whether the change was random or not.
1. Check how much did the sleep pattern change, did they move from 30 minutes to fall asleep to 30 seconds? If that's the case we might be up to something because this change was huge! If it was only from 30 minutes to 29 minutes then this could well be a random thing. The higher the change then we say the more significant it is, and we would give this significance a higher number.
So the first thing we check how much change did we have.
The second thing which we are going to check in order to estimate whether this change was just due to some random stuff going in their life or could be related actually to the pill we gave them is whether the set of results we got from them is very diversified or not.
For example if all of them reduced the time to sleep in exactly x minutes, i mean all of them then we have no variance in the results and this could be more suspiciously related to the pill.
However, if one guy reduced it by one second one by 29 minutes and for the third it raised, then we have a lot of variance and it's less likely that we can deduce something about the pill with strong significance.
Therefore, we have two items we measure in order to check whether we can make any claims about the hypothesis, how far is our average value from the original average value they had, the farther the more effect we got and more significant and how variant our measurements are with relation one to another the more diversified the less we can say it's significant.
So if you look at how we check for whether we can make any claims on our hypothesis with high significance what we are doing is looking at the results we got, compare them to the original result see how far it is, and how spread the results themselves are.
However, I skipped something important, which I didn't tell you yet. And it stands at the basis of significance check. When we look at the standard variation of our data, we don't just look at the standard variation of it, we look at the standard variation of the average value of all our measurements.
StdDev of Average Of Measruements.
Why is that? Why do we care about the stddev of the average of measurements and not the stddev of our measurements themself when talking about significance?
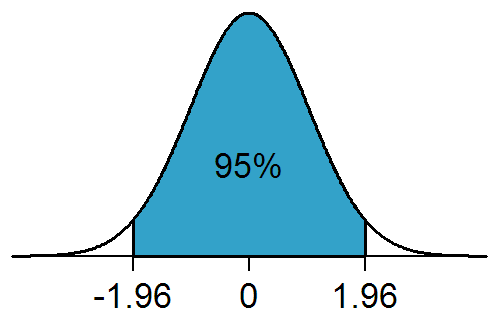
This is because it was proven and you can also intuitively see that the standard deviation of the mean decreases when we have more measurements.
This is because it does not matter the source distribution of the measurements when you check the average they always behave in normal distribution!
If you toss a coin and call the heads 1 and tails 0, then if you toss it 10 times then the chance of getting head or tail is 0.5 for each coin toss. It's uniform.
However, if you toss a coin 2 times and then sum the result and then toss another 2 time and sum the results than with the same 10 experiments if you count the sum of those experiments then the sum could be 10 but it could be 5 or could be 0 it's not only 1 or 0 for each toss.
So if we look at the average of these toss coins we get the normal distribution.
And this is because we look at average, or the sum of the results, when you look at some results and averages there are multiple possible outcomes, and they always behave in the normal distribution form.
So now that we know that our averages behave in a specific distribution form we can look at those results and deduce stuff we can tell hey this result was really off the normal distribution curve, there was so little chance this would happen this must be significant.
To sum up
The significance is a number, we calculate this number with formulas, however there is an intuition when you look at any of these statistical formulas that compute the significance of our experiment results you would always see that what they do is check how different the average that we got in the experiments is different from population average (if we know it) the higher this difference then the more significant our result is, however the higher the variation of the averages we got in our samples then this means our samples results are not stable and therefore it's more hard to conclude conclusions about experiment and therefore we have a lower significance.
Comments
Post a Comment